Summary

- Plugin name : Spectral Analysis
- Version : 1.2
- Author : Laurent Bonnet / Quentin Barthelemy
- Company : Mensia Technologies SA
- Short description : Performs a Spectral Analysis using FFT.
- Documentation template generation date : Jan 9 2018
Description
Performs a Spectral Analysis using FFT.
The Spectral Analysis box performs spectrum computations on incoming signals and possible outputs include the spectrum amplitude (the power of the signal in a number of frequency bands), as well as its phase, real part and imaginary part. Output computations may be enabled/disabled from the settings dialogue box. The analysis is performed using a Fast Fourier Transform . Do not forget to apply a Windowing step before spectral analysis.
Considering an input signal  , composed of
, composed of 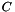 channels and
channels and  temporal samples, this plugin computes the spectrum of this signal
temporal samples, this plugin computes the spectrum of this signal 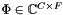 , composed of
, composed of 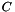 channels and
channels and 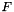 frequencies. Input signal being real, the spectrum exhibits conjugate symmetry: consequently, only half of the spectrum is returned with
frequencies. Input signal being real, the spectrum exhibits conjugate symmetry: consequently, only half of the spectrum is returned with 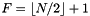 . For the
. For the 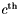 channel and the
channel and the 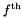 frequency, the spectrum is defined as:
frequency, the spectrum is defined as:
![\[ \Phi(c,f) = \Phi_r(c,f) + \mathsf{i} \times \Phi_i(c,f) = \left| \Phi(c,f) \right| \times e^{\mathsf{i} \arg(\Phi(c,f))} \]](form_20.png)
with 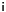 being the imaginary unit.
being the imaginary unit.
Using these notations, for the 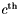 channel, the Parseval's Theorem gives:
channel, the Parseval's Theorem gives:
![\[ \sum_{n=0}^{N-1} \left| X(c,n) \right|^2 = \frac{1}{N} \sum_{f=0}^{F-1} \left| \Phi(c,f) \right|^2 \]](form_22.png)
with 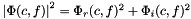 .
.
Inputs
1. Input signal
An input multichannel signal  , composed of
, composed of 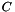 channels and
channels and  temporal samples.
temporal samples.
- Type identifier : Signal (0x5ba36127, 0x195feae1)
Outputs
1. Amplitude
An output spectral amplitude (absolute value) 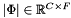 .
.
- Type identifier : Spectrum (0x1f261c0a, 0x593bf6bd)
2. Phase
An output spectral phase 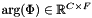 , in radians.
, in radians.
- Type identifier : Spectrum (0x1f261c0a, 0x593bf6bd)
3. Real Part
An output real part of the spectrum 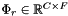 .
.
- Type identifier : Spectrum (0x1f261c0a, 0x593bf6bd)
4. Imaginary Part
An output imaginary part of the spectrum 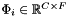 .
.
- Type identifier : Spectrum (0x1f261c0a, 0x593bf6bd)
Settings
1. Amplitude
Activate or not the Amplitude output.
- Type identifier : Boolean (0x2cdb2f0b, 0x12f231ea)
- Default value : [ true ]
2. Phase
Activate or not the Phase output.
- Type identifier : Boolean (0x2cdb2f0b, 0x12f231ea)
- Default value : [ false ]
3. Real Part
Activate or not the Real Part output.
- Type identifier : Boolean (0x2cdb2f0b, 0x12f231ea)
- Default value : [ false ]
4. Imaginary Part
Activate or not the Imaginary Part output.
- Type identifier : Boolean (0x2cdb2f0b, 0x12f231ea)
- Default value : [ false ]
Examples
Practical example : visualising the power spectrum of a signal.
Let's use a Signal Oscillator box to generator sinusoidal signals on one channel. Next we add a Spectral Analysis box and connect boxes together. We make sure the 'Amplitude' of the signal is computed by checking the appropriate setting in the settings dialog box (see image below). Finally, we connect the 'Amplitude' output connector of the Spectral Analysis box to the input connector of a Power Spectrum Display box. The player may now be launched to visualize the power spectrum of the signal.
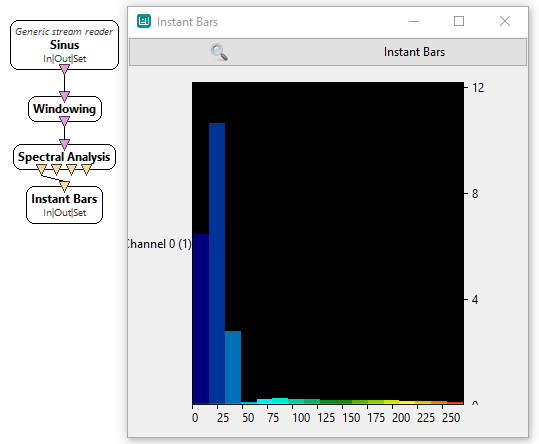
Miscellaneous
To verify the Parseval's Theorem, in version 1.1, spectra have been multiplied by 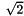 with respect the previous version 1.0. DC bin and Nyquist bin (when
with respect the previous version 1.0. DC bin and Nyquist bin (when  is even) are not concerned by this correction.
is even) are not concerned by this correction.
Generated on Tue Jun 26 2012 15:25:54 for Documentation by
 1.7.4
1.7.4
